Apa itu kontroler atau kendali PID?

Berdasarkan survey yang di lakukan oleh Desborough dan Miller di tahun 2002 terhadap lebih dari 11 ribu perusahaan yang bergerak di bidang manufaktur seperti perusahaan pembuatan kertas, sebanyak 97% perusahan menggunakan kontroler PID sebagai kontroler dari mesin-mesin mereka [1]. Berdasarkan survey tersebut, membuktikan bahwa kontroler PID sudah teruji baik secara performa maupun robustness dalam menangani sistem yang kompleks. Oleh sebab itu, pada postingan kali ini, saya akan menjelaskan apa itu kontroler PID.

Kontroler PID terdiri dari tiga aksi kontrol, yaitu kontrol proporsional (P), integral (I), dan derivatif (D) seperti yang ditunjukkan pada Gambar 1. Dalam implementasinya, kontroler PID tidak selalu digunakan bersamaan dan tergantung dari kebutuhan, misalnya kita dapat menggunakan kontroler P saja, kombinasi P dan I yang dikenal dengan kontroler PI, atau kombinasi P dan D yang dikenal dengan kontroler PD.

Gambar 1. Kontroler PID.

Kontroler proporsional (P)

Aksi kontrol dari kontroler proporsional (P) bergantung pada error saat ini. Disebut kontroler proporsional karena aksi kontrol dari kontroler ini proporsional dengan nilai error yang merupakan masukan dari kontroler. Jadi, jika error sama dengan nol maka aksi kontrol dari kontroler proporsional sama dengan nol juga. Sehingga, persamaan dari kontroler proporsional dapat di tulisakan sebagai berikut.

$$ U_{p}(s)=k_{p}\cdot e(s) $$

$$ U_{p}(t)=k_{p}\cdot e(t) $$

\(U_{p}\): aksi kontrol proporsional.

\(k_{p}\): gain proporsional.

\(e = r - y\): error.

\(r\): setpoint. 

\(y\): keluaran sistem.

Kontroler Integral (I)

Aksi kontrol dari kontroler integral (I) bergantung pada error sebelumnya. Disebut kontroler integral karena kontroler ini menjumlahkan error sepanjang waktu. Dengan kata lain, jika error saat ini adalah nol, maka aksi kontroler ini tidak sama dengan nol. Oleh sebab itu, kontroler ini mampu menghilangkan error steady state atau offset. Jika gain kontroler integral di desain sebaik mungkin, maka dengan penambahan kontroler ini mampu membuat error menjadi nol jika sistem diberikan gangguan yang konstan. Namun, kontroler integral juga dapat membuat sistem berosilasi. Selain itu, kontroler integral juga rentan terhadap sistem yang mempunya saturasi.

$$ U_{i}(s)=\frac{k_{i}}{s}\cdot e(s) $$

$$ U_{i}(t)=k_{i}\cdot \int_{0}^{t}e(\tau )d\tau $$

\(U_{i}\): aksi kontrol integral.

\(k_{i}\): gain integral.

Kontroler Derivatif (D)

Aksi kontrol dari kontroller derivatif (D) bergantung pada error rate (derivatif dari error). Fungsi alih dari kontroler derivatif dapat dituliskan sebagai berikut.

$$ U_{d}(s)=k_{d}\cdot s \cdot e(s) $$

$$ U_{d}(t)=k_{d}\cdot \frac{de(t)}{dt}$$

\(U_{d}\): aksi kontrol derivatif.

\(k_{d}\): gain derivatif.

Karena bergantung pada derivatif dari error, kontroler ini mempunyai kemampuan untuk mengantisipasi atau memprediksi error dengan linear extrapolation. Bagaimana kontroler derivatif memprediksi error? Untuk menjelaskannya, kita representasikan error ke dalam domain waktu seperti yang di jelaskan oleh [1].

$$e(t+T_{d})\approx e(t)+T_{d}\frac{de(t)}{dt}$$

\(T_{d}\): perkiraan waktu dimana error di proyeksikan ke depan.

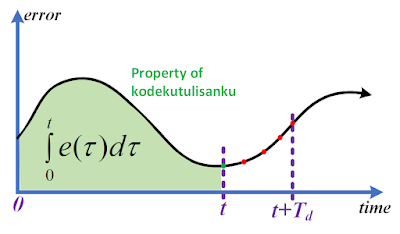Gambar 2. Error sinyal.

Sebagai contoh, error pada sistem mengalami penurunan dengan kecepatan \(\frac{de(t)}{dt}=5\), sedangkan gain kontroler derivatif \(k_{d}=2\). Sehingga, aksi kontrol derivatif adalah sebesar \(U_{d}=-10\). Kenapa aksi kontrol derivatif minus? karena error mengalami penurunan. Ketika aksi kontrol derivatif minus, ini akan membuat respon sistem melambat ketika mendekati setpoint. Oleh sebab itu, kontroler derivatif mampu mengurangi overshoot. Menurut [2], aksi kontrol derivatif sangat memiliki pengaruh yang besar pada sistem orde 2 dari pada sistem orde 1. Namun, ketika sistem terdapat noise (derau) maka kontroler derivatif akan membawa dampak buruk. Hal ini disebabkan oleh kontrol derivatif bergantung pada derivatif dari error.

Struktur Kontroler PID

Kontrol PID memiliki 2 struktur, yaitu paralel dan seri yang akan dijelaskan dibagian ini.

Kontroler PID Paralel 

Gambar 1 menunjukkan kontroler PID dengan struktur standar, ideal, atau paralel yang mana fungsi alihnya dapat dituliskan sebagai berikut.

$$ C(s)=\frac{U_{pid}(s)}{e(s)}=k_{p}+\frac{k_{i}}{s}+k_{d}s $$

Jika \(k_{i}=\frac{k_{p}}{T_{i}}\) dan \(k_{d}=k_{p}T_{d}\), maka

$$ C(s)=\frac{U_{pid}(s)}{e(s)}=k_{p}\left ( 1+\frac{1}{T_{i}s}+T_{d}s \right ) $$

\(T_{i}\): waktu integral.

\(T_{d}\): waktu derivatif.

Kontroler PID Seri

Struktur kontroler PID seri dapat dilihat pada Gambar 3.

Gambar 3. Kontroler PID seri.

Dari Gambar 3, fungsi alih dari kontroler PID seri dapat dituliskan sebagai berikut.

$$ C(s)=\frac{U_{pid}(s)}{e(s)}=\left ( \alpha +T_{d}s \right )k_{p}\left ( 1+\frac{1}{\alpha T_{i}s} \right ) $$

Dimana nilai \( \alpha\) didapatkan dari

$$ \alpha =\frac{1\pm \sqrt{1-4\frac{T_{d}}{T_{i}}}}{2}>0 $$

Daftar Pustaka

[1] K. J. Åström and R. M. Murray, Feedback systems: an introduction for scientists and engineers. Princeton university press, 2021.

[2] Y. Li, K. H. Ang, and G. C. Chong, "PID control system analysis and design," IEEE Control Systems Magazine, vol. 26, no. 1, pp. 32-41, 2006.